Hello everyone, I am here to do a little guest blogging today. Instead of some useful empirical tools or interesting analysis, I want to take you on a short tour through of the murkier aspects of economic theory: anticipation. The very idea of the ubiquitous Nash Equilibrium is rooted in anticipation. Much of behavioral economics is focused on determining how people anticipate one another’s actions. While economists have a pretty decent handle on how people will anticipate and act in repeated games (the same game played over and over) and small games with a few different decisions, not as much work has been put into studying long games with complex history dependence. To use an analogy, economists have done a lot of work on games that look like poker but much less work on games that look like chess.
One of the fundamental problems is finding a long form game that has enough mathematical coherence and deep structure to allow the game to be solved analytically. Economists like analytical solutions when they are available, but it is rare to find an interesting game that can be solved by pen and paper.
Brute force simulation can be helpful. Simply simulating all possible outcomes and using a technique called backwards induction, we can solve the game in a Nash Equilibrium sense, but this approach has drawbacks. First, the technique is limited. Even with a wonderful computer and a lot of time, there are some games that simply cannot be solved in human time due to their complexity. More importantly, any solutions that are derived are not realistic. The average person does not have the ability to perform the same computations as a super computer. On the other hand, people are not as simple as the mechanical actions of a physics inspired model.
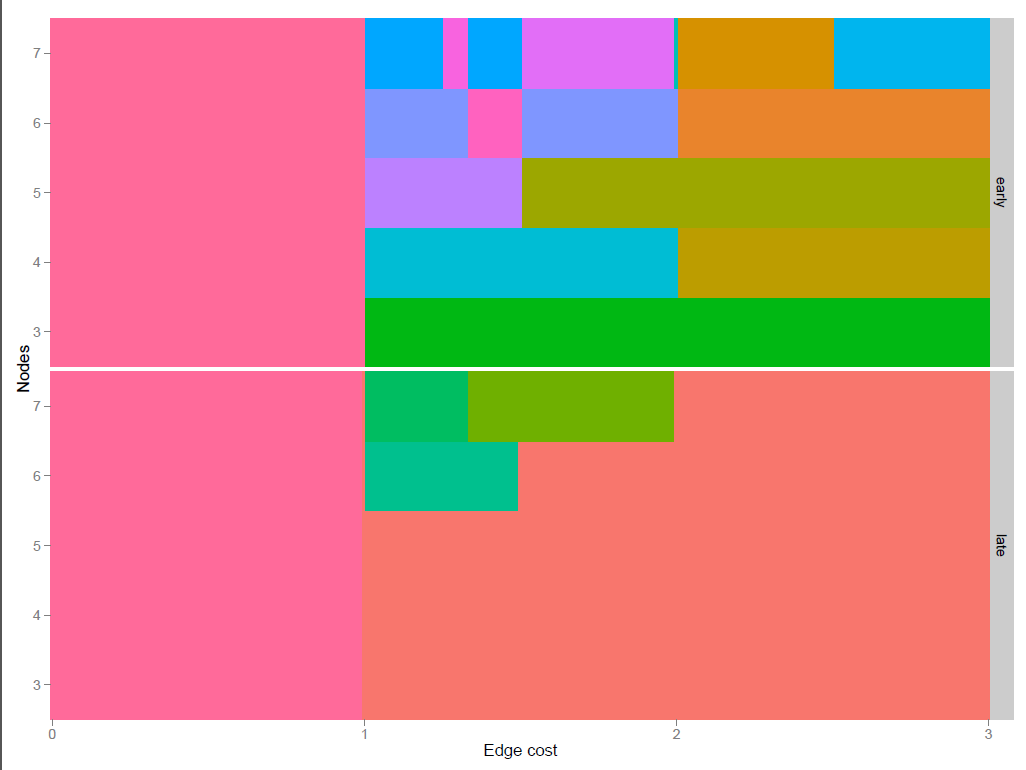
James and I have been working on a game of strategic network formation which effectively illustrates all these problems. The model takes 2 parameters (the number of nodes and the cost of making new connections) and uses them to strategically construct a network in a decentralized way. The rules are extremely simple and almost completely linear, but the complexities of backwards induction make it impossible to solve by hand for a network of any significant size (some modifications can be added which shrink the state space to the point where the game can be solved). Backwards induction doesn’t work for large networks, since the number of possible outcomes grows at a rate of (roughly) but what we can see is intriguing. The results seem to follow a pattern, but they are not predictable.
Each region of a different color represents a different network (colors selected based on network properties). The y-axis is discrete number of nudes in the network. The x axis is a continuous cost parameter. Compare where the color changes as the cost parameter is varied across the different numbers of nodes. As you can see, switch points tend to be somewhat similar across network scales, but they are not completely consistent.
Currently we are exploring a number of options; I personally think that agent-based modeling is going to be the key to tackling this type of problem (and those that are even less tractable) in the future. Agent based models and genetic algorithms have the potential to be more realistic and more tractable than any more traditional solution.